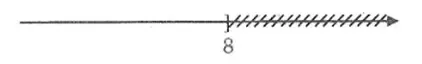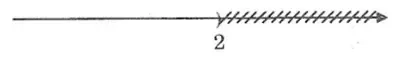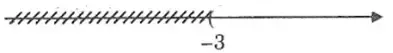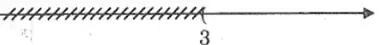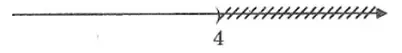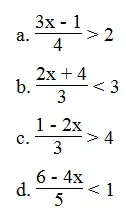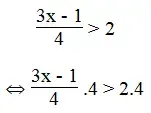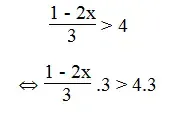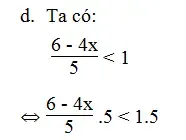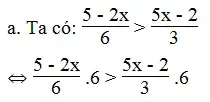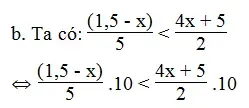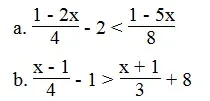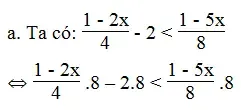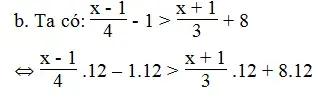Tập nghiệm của bất phương trình 6x 2 x + 1 0 Đầy đủ
Mẹo Hướng dẫn Tập nghiệm của bất phương trình 6x 2 x + 1 0 2022
You đang tìm kiếm từ khóa Tập nghiệm của bất phương trình 6x 2 x + 1 0 được Update vào lúc : 2022-04-10 08:18:09 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Sách Giải Sách Bài Tập Toán 8 Bài 4: Bất phương trình bạc nhất một ẩn giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 8 sẽ hỗ trợ bạn rèn luyện kĩ năng suy luận hợp lý và hợp logic, hình thành kĩ năng vận dụng kết thức toán học vào đời sống và vào những môn học khác:
a. x – 2 > 4
b. x + 5 < 7
c. x – 4 < -8
d. x + 3 > – 6
Lời giải:
a. Ta có: x – 2 > 4 ⇔ x > 4 + 2 ⇔ x > 6
Vậy tập nghiệm của bất phương trình là: x > 6
b. Ta có: x + 5 < 7 ⇔ x < 7 – 5 ⇔ x < 2
Vậy tập nghiệm của bất phương trình là: x < 2
c. Ta có: x – 4 < -8 ⇔ x < -8 + 4 ⇔ x < -4
Vậy tập nghiệm của bất phương trình là: x
d. Ta có: x + 3 > -6 ⇔ x > -6 – 3 ⇔ x > -9
Vậy tập nghiệm của bất phương trình là: x > -9
a. 3x < 2x + 5
b. 2x + 1 < x + 4
c. -2x > -3x + 3
d. -4x – 2 > -5x + 6
Lời giải:
a. Ta có: 3x < 2x + 5 ⇔ 3x – 2x < 5 ⇔ x < 5
Vậy tập nghiệm của bất phương trình là: x
b. Ta có: 2x + 1 < x + 4 ⇔ 2x – x < 4 – 1 ⇔ x < 3
Vậy tập nghiệm của bất phương trình là: x < 3
c. Ta có: -2x > -3x + 3 ⇔ -2x + 3x > 3 ⇔ x > 3
Vậy tập nghiệm của bất phương trình là: x > 3
d. Ta có: -4x – 2 > -5x + 6 ⇔ -4x + 5x > 6 + 2 ⇔ x > 8
Vậy tập nghiệm của bất phương trình là: x > 8
a. 1/2 x > 3
b. -1/3 < -2
c. 2/3 x > -4
d. – 3/5 x > 6
Lời giải:
a. Ta có: 1/2 x > 3 ⇔ 1/2 x.2 > 3.2 ⇔ x > 6
Vậy tập nghiệm của bất phương trình là: x > 6
b. Ta có: -1/3 < -2 ⇔ -1/3 x.(-3) > (-2).(-3) ⇔ x > 6
Vậy tập nghiệm của bất phương trình là: x
c. Ta có: 2/3 x > -4 ⇔ 2/3 x. 3/2 > -4. 3/2 ⇔ x > -6
Vậy tập nghiệm của bất phương trình là: x > -6
d. Ta có: -3/5 x > 6 ⇔ -3/5 x.(-5/3 ) < 6.(-5/3 ) ⇔ x < -10
Vậy tập nghiệm của bất phương trình là: x
a. 3x < 18
b. -2x > -6
c. 0,2x > 8
d. -0,3x < 12
Lời giải:
a. Ta có: 3x < 18 ⇔ 3x. 13 < 18. 13 ⇔ x < 6
Vậy tập nghiệm của bất phương trình là: x
b. Ta có: -2x > -6 ⇔ -2x.(- 12 ) < -6.(- 12 ) ⇔ x < 3
Vậy tập nghiệm của bất phương trình là: x
c. Ta có: 0,2x > 8 ⇔ 0,2x.5 > 8.5 ⇔ x > 40
Vậy tập nghiệm của bất phương trình là: x > 40
d. Ta có: -0,3x < 12 ⇔ – 310 x.(- 103 ) > 12.(- 103 ) ⇔ x > -40
Vậy tập nghiệm của bất phương trình là: x
a. 2x < 3 ⇔ 3x < 4,5
b. x – 5 < 12 ⇔ x + 5 < 22
c. -3x < 9 ⇔ 6x > -18
Lời giải:
a. Nhân hai vế của bất phương trình 2x < 3 với cùng 1,5.
b. Cộng hai vế của bất phương trình x – 5 < 12 với 10.
c. Nhân hai vế của bất phương trình -3x < 9 với -2.
Bạn An nhận định rằng, hình vẽ đó màn biểu diễn tập nghiệm của bất phương trình 2x ≤ 16, còn bạn Bình lại xác lập hình vẽ đó màn biểu diễn tập nghiệm của bất phương trình x + 2 ≤ 10. Theo em bạn nào đúng?
Lời giải:
Ta có: 2x ≤ 16 ⇔ x ≤ 8
x + 2 ≤ 10 ⇔ x ≤ 8
Như vậy cả hai bạn đều phát biểu đúng.
a. 2x – 4 < 0
b. 3x + 9 > 0
c. –x + 3 < 0
d. -3x + 12 > 0
Lời giải:
a. Ta có: 2x – 4 < 0 ⇔ 2x < 4 ⇔ x < 2
b. Ta có: 3x + 9 > 0 ⇔ 3x > -9 ⇔ x > -3
c. Ta có: -x + 3 < 0 ⇔ -x < -3 ⇔ x > 3
d. Ta có: -3x + 12 > 0 ⇔ -3x > -12 ⇔ x < 4
a. 3x + 2 > 8
b. 4x – 5 < 7
c. -2x + 1 < 7
d. 13 – 2x > -2
Lời giải:
a. Ta có: 3x + 2 > 8 ⇔ 3x > 8 – 2 ⇔ 3x > 6 ⇔ x > 2
Vậy tập nghiệm của bất phương trình là: x
b. Ta có: 4x – 5 < 7 ⇔ 4x < 7 + 5 ⇔ 4x < 12 ⇔ x < 3
Vậy tập nghiệm của bất phương trình là: x
c. Ta có: -2x + 1 < 7 ⇔ -2x < 7 – 1 ⇔ -2x < 6 ⇔ x > -3
Vậy tập nghiệm của bất phương trình là: x > -3
d. Ta có: 13 – 2x > -2 ⇔ -3x > -2 – 13 ⇔ -3x > -15 ⇔ x < 5
Vậy tập nghiệm của bất phương trình là: x < 5
a. 3/2 x < -9
b. 5 + 2/3 x > 3
c. 2x + 4/5 > 9/5
d. 6 – 3/5 x < 4
Lời giải:
a. Ta có: 32 x < -9 ⇔ 3/2 x. 2/3 < -9.(2/3 ) ⇔ x < -6
Vậy tập nghiệm của bất phương trình là: x
b. Ta có: 5 + 2/3 x > 3 ⇔ 2/3 x > 3 – 5 ⇔ 2/3 x. 3/2 > -2. 3/2 ⇔ x > -3
Vậy tập nghiệm của bất phương trình là: x > -3
c. Ta có: 2x + 4/5 > 95 ⇔ 2x > 9/5 – 4/5 ⇔ 2x > 1 ⇔ x > 1/2
Vậy tập nghiệm của bất phương trình là: x > 1/2
d. Ta có: 6 – 3/5 x < 4 ⇔ -3/5 x < 4 – 6 ⇔ -3/5 x.(-5/3 ) > -2.(-5/3 ) ⇔ x > 10/3
Vậy tập nghiệm của bất phương trình là: x
a. 7x – 2,2 < 0,6
b. 1,5 > 2,3 – 4x
Lời giải:
a. Ta có: 7x – 2,2 < 0,6
⇔ 7x < 0,6 + 2,2
⇔ 7x < 2,8
⇔ x < 0,4
Vậy tập nghiệm của bất phương trình là: x < 0,4
b. Ta có: 1,5 > 2,3 – 4x
⇔ 4x > 2,3 – 1,5
⇔ 4x > 0,8
⇔ x > 0,2
Vậy tập nghiệm của bất phương trình là: x
Lời giải:
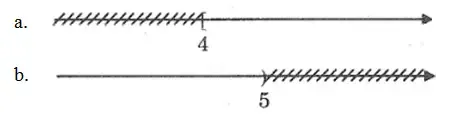
a. Bất phương trình số 1 một ẩn có tập nghiệm màn biểu diễn bởi hình vẽ là:
2x – 8 ≥ 0
b. Bất phương trình số 1 một ẩn có tập nghiệm màn biểu diễn bởi hình vẽ là:
3x – 15 < 0
Lời giải:
a. Ta có:
⇔ 3x – 1 > 8
⇔ 3x > 8 + 1
⇔ 3x > 9 ⇔ x > 3
Vậy tập nghiệm của bất phương trình là: x
b. Ta có:
⇔ 2x + 4 < 9
⇔ 2x < 9 – 4
⇔ 2x < 5 ⇔ x < 2,5
Vậy tập nghiệm của bất phương trình là: x
c. Ta có:
⇔ 1 – 2x > 12
⇔ -2x > 12 – 1
⇔ -2x > 11 ⇔ x < -5,5
Vậy tập nghiệm của bất phương trình là: x < -5,5
d. Ta có:
⇔ 6 – 4x < 5
⇔ -4x < 5 – 6
⇔ -4x < -1 ⇔ x > 1/4
Vậy tập nghiệm của bất phương trình là: x
a. (x – 1)2 < x(x – 3)
b. (x – 2)(x + 2) > x(x – 4)
c. 2x + 3 < 6 – (3 – 4x)
d. -2 – 7x > (3 + 2x) – (5 – 6x)
Lời giải:
a. Ta có: (x – 1)2 < x(x – 3) ⇔ x2 – 2x + 1 < x2 – 3x
⇔ x2 – 2x + 1 – x2 + 3x < 0
⇔ x + 1 < 0 ⇔ x < -1
Vậy tập nghiệm của bất phương trình là: x
b. Ta có: (x – 2)(x + 2) > x(x – 4) ⇔ x2 – 4 > x2 – 4x
⇔ x2 – 4 – x2 + 4x > 0
⇔ 4x – 4 > 0 ⇔ x > 1
Vậy tập nghiệm của bất phương trình là: x
c. Ta có: 2x + 3 < 6 – (3 – 4x) ⇔ 2x + 3 < 6 – 3 + 4x
⇔ 2x – 4x < 3 – 3
⇔ -2x < 0 ⇔ x > 0
Vậy tập nghiệm của bất phương trình là: x
d. Ta có: -2 – 7x > (3 + 2x) – (5 – 6x) ⇔ -2 – 7x > 3 + 2x – 5 + 6x
⇔ -7x – 2x – 6x < 3 – 5 + 2
⇔ -15x > 0 ⇔ x < 0
Vậy tập nghiệm của bất phương trình là: x < 0
a. Giá trị phân thức (5 – 2x)/6 to nhiều hơn giá trị phân thức (5x – 2)/3
b. Giá trị phân thức (1,5 – x)/5 nhỏ hơn giá trị phân thức (4x + 5)/2
Lời giải:
⇔ 5 – 2x > 10x – 4
⇔ -2x – 10x > -4 – 5⇔ -12x > -9⇔ x < 3/4
Vậy với x < 3/4 thì giá trị phân thức (5 – 2x)/6 to nhiều hơn giá trị phân thức (5x – 2)/3
⇔ 3 – 2x < 20x + 25⇔ -2x – 20x < 25 – 3
⇔ -22x < 22⇔ x > -1
Vậy với x > -1 thì giá trị phân thức (1,5 – x)/5 nhỏ hơn giá trị phân thức 4x + 5)/2 .
Lời giải:
Ta có: 5 – 3x < (4 + 2x) – 1 ⇔ 5 – 3x < 4 + 2x – 1
⇔ -3x – 2x < 4 – 1 – 5 ⇔ -5x < -2 ⇔ x > 2/5
Vậy chỉ có mức giá trị 2/3 > 2/5 nên trong những số đã cho thì số 2/3 là nghiệm của bất phương trình.
Lời giải:
Ta có, quy tắc chuyển vế của phương trình giống quy tắc chuyển vế của bất phương trình, nhưng quy tắc nhân hai vế của phương trình với cùng một số trong những khác 0 không thể chuyển thành quy tắc nhân hai vế của bất phương trình với cùng một số trong những khác 0, chính bới bất phường trình sẽ đổi chiều khi ta nhân hai vế của nó với một số trong những âm.
a. Chứng tỏ những giá trị -5; 0; -8 đều không phải là nghiệm của nó.
b. Bất phương trình này hoàn toàn có thể nhận giá trị nào của x là nghiệm?
Lời giải:
a. Thay giá trị của x vào từng vế của bất phương trình:
x = -5 vế trái: 2.(-5) + 1 = -10 + 1 = -9
vế phải: 2.[(-5) + 1] = 2.(-4) = -8
Vì -9 < -8 nên x = -5 không phải là nghiệm của bất phương trình.
x = 0 vế trái: 2.0 + 1 = 1
vế phải: 2.(0 + 1) = 2
Vì 1 < 2 nên x = 0 không phải là nghiệm của bất phương trình.
x = -8 vế trái: 2.(-8) + 1 = -16 + 1 = -15
vế phải: 2.[(-8) + 1] = 2.(-7) = -14
Vì -15 < -14 nên x = -8 không là nghiệm của bất phương trình.
b. Ta có: 2x + 1 > 2(x + 2)
⇔ 2x + 1 > 2x + 2
⇔ 0x > 1
Vậy bất phương trình vô nghiệm.
Lời giải:
Ta có: 5 + 5x < 5(x + 2)
⇔ 5 + 5x < 5x + 10
⇔ 5x – 5x < 10 – 5
⇔ 0x < 5
Bất kì giá trị nào của x cũng thỏa mãn nhu cầu vế trái nhỏ hơn vế phải.
Vậy tập nghiệm của bất phương trình là tập số thực R.
a. x < 5 ⇔ (a – b)x < 5(a – b)
b. x > 2 ⇔ (a – b)x < 2(a – b)
Lời giải:
a. Ta có: x < 5 ⇔ (a – b)x < 5(a – b)
⇒ a – b > 0 ⇔ a > b
b. Ta có: x > 2 ⇔ (a – b)x < 2(a – b)
⇒ a – b < 0 ⇔ a < b
a. 5,2 + 0,3x < – 0,5
b. 1,2 – (2,1 – 0,2x) < 4,4
Lời giải:
a. Ta có: 5,2 + 0,3x < – 0,5
⇔ 0,3x < – 0,5 – 5,2
⇔ 0,3x < – 5,7
⇔ x < -19
Vậy số nguyên lớn số 1 cần tìm là -20
b. Ta có: 1,2 – (2,1 – 0,2x) < 4,4
⇔ 1,2 -2,1 + 0,2x < 4,4
⇔ 0,2x < 4,4 – 1,2 + 2,1
⇔ 0,2x < 5,3
⇔ x < 53/2
Vậy số nguyên lớn số 1 thỏa mãn nhu cầu Đk là số 26.
a. 0,2x + 3,2 > 1,5
b. 4,2 – (3 – 0,4x) > 0,1x + 0,5
Lời giải:
a. Ta có: 0,2x + 3,2 > 1,5
⇔ 0,2x > 1,5 – 3,2
⇔ 0,2x > – 1,7
⇔ x > – 17/2
Vậy số nguyên nhỏ nhất cần tìm là – 8.
b. Ta có: 4,2 – (3 – 0,4x) > 0,1x + 0,5
⇔ 4,2 – 3 + 0,4x > 0,1x + 0,5
⇔ 0,4x – 0,1x > 0,5 – 1,2
⇔ 0,3x > – 0,7
⇔ x > – 7/3
Vậy số nguyên nhỏ nhất cần tìm là -2.
a. x – 3 = 2m + 4 có nghiệm dương?
b. 2x – 5 = m + 8 có nghiệm số âm?
Lời giải:
a. Ta có x – 3 = 2m + 4
⇔ x = 2m + 4 + 3
⇔ x = 2m + 7
Phương trình có nghiệm số dương khi 2m + 7 > 0 ⇔ m > – 7/2
b. Ta có: 2x – 5 = m + 8
⇔ 2x = m + 8 + 5
⇔ 2x = m + 13
⇔ x = -(m + 13)/2
Phương trình có nghiệm số âm khi -(m + 13)/2 < 0 ⇔ m + 13 < 0 ⇔ m < -13
a. (x + 2)2 < 2x(x + 2) + 4
b. (x + 2)(x + 4) > (x – 2)(x + 8) + 26
Lời giải:
a. Ta có: (x + 2)2 < 2x(x + 2) + 4
⇔ x2 + 4x + 4 < 2x2 + 4x + 4
⇔ x2 + 4x – 2x2 – 4x < 4 – 4
⇔ -x2 < 0
⇔ x2 > 0
Vậy tập nghiệm của bất phương trình là: x
b. Ta có: (x + 2)(x + 4) > (x – 2)(x + 8) + 26
⇔ x2 + 4x + 2x + 8 > x2 + 8x – 2x – 16 + 26
⇔ x2 + 6x – x2 < 10 – 8
⇔ 0x > 2
Vậy bất phương trình vô nghiệm.
Lời giải:
⇔ 2 – 4x – 16 < 1 – 5x
⇔ -4x + 5x < 1 – 2 + 16
⇔ x < 15
Vậy tập nghiệm của bất phương trình là: x
⇔ 3x – 3 – 12 > 4x + 4 + 96
⇔ 3x – 4x > 4 + 96 + 3 + 12
⇔ -x > 115 ⇔ x < -115
Vậy tập nghiệm của bất phương trình là: x
a. 3(5 – 4n) + (27 + 2n) > 0
b. (n + 2)2 – (n – 3)(n + 3) ≤ 40
Lời giải:
a. Ta có: 3(5 – 4n) + (27 + 2n) > 0
⇔ 15 – 12n + 27 + 2n > 0
⇔ -10n + 42 > 0
⇔ -10n > -42
⇔ n < 4,2
Vậy những số tự nhiên cần tìm là 0; 1; 2; 3; 4.
b. Ta có: (n + 2)2 – (n – 3)(n + 3) ≤ 40
⇔ n2 + 4n + 4 – n2 + 9 ≤ 40
⇔ 4n < 40 – 13
⇔ n < 27/4
Vậy những số tự nhiên cần tìm là 0; 1; 2; 3; 4; 5; 6.
Bất phương trình x – 2 < 1 tương tự với bất phương trình sau:
A. x > 3
B. x ≤ 3
C. x−1 >2
D. x – 1 < 2
Lời giải:
Chọn D
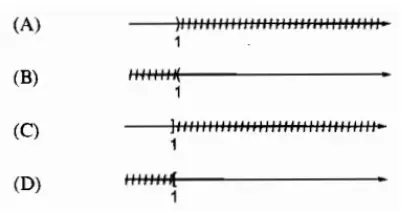
Bất phương trình số 1 2x – 1 > 1 có tập nghiệm màn biểu diễn bởi hình vẽ sau:
Lời giải:
Chọn B
a. x – 2 = 3m + 4 có nghiệm to nhiều hơn 3
b. 3 – 2x = m – 5 có nghiệm nhỏ hơn -2
Lời giải:
a. x – 2 = 3m + 4
⇔x = 3m + 6
Phương trình x – 2 = 3m + 4 có nghiệm to nhiều hơn 3 khi và chỉ khi: 3m + 6 > 3.
Giải: 3m + 6 > 3 có m > -1
Vậy với m > -1 thì phương trình ẩn x là x – 2 = 3m + 4 có nghiệm to nhiều hơn 3.
b. Với m > 12 thì phương trình ẩn x là 3 – 2x = m – 5 có nghiệm nhỏ hơn -2
a. 2x + 1 > 3 và |x| > 1
b. 3x – 9 < 0 và x2 < 9
Lời giải:
a. Giải bất phương trình 2x + 1 > 3 ta tìm kiếm được tập nghiệm là x > 1
Ta kiểm tra được x = -2 là nghiệm của bất phương trình nhưng không là nghiệm của 2x + 1 > 3 (không thuộc tập nghiệm x > 1)
Vậy hai bất phương trình 2x + 1 > 3 và
|x| > 1 không tương tự.
b. Kiểm tra giá tốt trị x = -4 là nghiệm của 3x – 9 < 0 nhưng không là nghiệm của x2 < 9.
Share Link Cập nhật Tập nghiệm của bất phương trình 6x 2 x + 1 0 miễn phí
Bạn vừa đọc Post Với Một số hướng dẫn một cách rõ ràng hơn về Video Tập nghiệm của bất phương trình 6x 2 x + 1 0 tiên tiến và phát triển nhất và ShareLink Tải Tập nghiệm của bất phương trình 6x 2 x + 1 0 Free.